凹面光栅既是色散元件,又是成像系统,构成的光学系统更简单,在光谱仪中应用也更为广泛。分辨率是光谱仪最重要的指标之一,因此在装调前需要对凹面光栅进行检测^[1]。凹面光栅的使用条件不同于平面光栅,其入射波和衍射波均为球面波,入射角度、入臂和出臂的长度,即光栅、入缝和探测器三者的位置,是经过消像差设计得出的^[2],不可随意放置。这给凹面光栅的检测带来困难,要根据不同凹面光栅的使用参数来构建检测系统。虽然现有的光学系统设计软件采用光线追迹法,根据点列图或对比传递函数MTF来评估系统的分辨率,但是由于制造安装的误差,实际分辨率要低于理论值。目前,文献中有关于凹面光栅衍射效率的理论计算研究的^{[3, 4]},也有较多文献关注对影响凹面光栅分辨率的因素进行理论分析的,而对于分辨率检测方法的理论与实验进行综合分析研究,得出真正凹面光栅分辨率而非带入系统影响因素的研究还没有具体文献。若仅从缝光源宽度、光栅宽度及入缝宽度与分辨率的关系做定性研究,分析光栅实际分辨率恒小于理想分辨率的结论,并没有深入具体考虑整个分辨率检测系统各个因素对分辨率的综合影响,具有局限性^{[5, 6, 7]}。本文主要定量分析了检测系统中光源带宽、狭缝宽度及探测器各个参数对分辨率的影响,结合罗兰型凹面光栅的成像特点,计算宽波段使用范围内的凹面光栅实际分辨率。

要检测一块凹面光栅的分辨率,必须构建符合此光栅使用条件的检测系统,而检测系统的光源、狭缝和探测器以及其放置位置的精度不可避免地影响光栅检测结果。因此为了得到真正的凹面光栅分辩率必须对这些影响因素加以科学的分析,并在检测数据里,合理地加以去除。

凹面光栅的分辨率是指以点或线单色光源入射时,在像面上按照瑞利准则可分辨的最小光谱范围。在实际检测中没有这种光源,总是带有一定的尺寸大小和光谱带宽,因此应考虑它们对分辨率的影响。检测系统的光源采用标准汞灯,检测波段为200～1 000 nm。汞灯出光用光纤耦合,用聚光透镜将光斑聚焦在狭缝中心上,以近似点光源发散球面波入射到凹面光栅表面。必须注意的是入射光经光栅衍射的特征谱线事实上有一定的带宽;狭缝上的聚焦光点也有一定的尺寸大小;经过狭缝的入射球面波必须充满整个光栅表面,才能正确检测出光栅的光谱分辨本领。

如图 1所示,假设入射单色光波长λ存在一个很小的谱线带宽为δλ,入射角为α,衍射角为β。在不考虑像差时光栅理论最小可分辨角为 ,其中N为总刻线数,e为有效刻线数。如果考虑像差,则其主极大的半波光谱宽度为 ^[8]，其中δ为像差斑的半径,k为衍射级次。这就是要检测的凹面光栅的光谱分辨率。由于光源的非单色性,检测到的光谱半波宽度为(Δλ_G+δλ),因此在检测的数据中要剔除量δλ。

图 1

Fig. 1

图 1 光源展宽与衍射像的关系 Fig. 1 The relationship between light broadening and diffraction image

实验中采用的低压汞灯是气体放电光源,其原子谱线并非一条严格的几何线,无论是发射线还是吸收线,都具有一定的形状,即谱线轮廓。谱线的强度随频率的改变而改变,定义|v₂-v₁|的值Δv₀为频谱宽度,如图 2所示。

图 2

Fig. 2

图 2 原子频谱宽度 Fig. 2 The spectrum width of atomic

假设光波的波列长度为2 L,则由傅里叶频谱分析可知单色光λ的谱线宽度与波列长度的关系为 低压汞灯的蒸汽压只有1.3~13 Pa,其谱线增宽主要是多普勒增宽,谱宽为 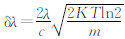,其中c为光速,K为波尔兹曼常数,T为热力学温度,m为原子或分子的质量^[9]。低压汞灯谱线在300 K时的理论多普勒增宽如表 1所示。

表 1Table 1)

表 1 低压汞灯谱线的多普勒增宽 Tab. 1 The Doppler broadening of low-pressure mercury lamp (300 K) 波长/nm 365.0 404.7 435.8 546.1 577.0 579.0 Δλ/nm 0.000 32 0.000 36 0.000 38 0.000 48 0.000 51 0.000 51

表 1 低压汞灯谱线的多普勒增宽 Tab. 1 The Doppler broadening of low-pressure mercury lamp

理想的点线光源是不存在的,要给光栅一定的光通量,那么狭缝一定要有大小。系统分辨率虽然随狭缝宽度调小而变高,测的光栅分辨率也越精确,但由于检测的光能量太小,信噪比低,这样就降低了测量的灵敏度,同时也降低测量的正确性。因此需要同时考虑光源和探测器的性能以及被测光栅的特性选择一个合理的狭缝宽度。如图 3所示,若入射狭缝的宽度为A₁A₂=a,其波长为λ的衍射像为B₁B₂=b,则光栅的衍射像 ,其对于检测带来的分辨率降低的理论影响值为b/2线宽度对应的光谱宽度。应用色散公式可以计算出狭缝宽度在光栅检测中带入的光谱展宽 ,因此在实际测量值中要减去该值。

图 3

Fig. 3

图 3 加狭缝光栅衍射示意图 Fig. 3 The grating diffraction with slit

选定波长为435.8 nm,通过调节狭缝的不同宽度来分析其对光栅分辨率检测的影响。图 4分别是狭缝宽度为5 μm、10 μm、50 μm、100 μm时检测结果对照图。从实验结果可以看出,不同狭缝宽度对检测结果影响很大。狭缝宽度a=5 μm时,Δλ=0.016 5 nm;a=10 μm时,Δλ=0.017 7 nm;a=50 μm时,Δλ=0.021 0 nm;a=100 μm时,Δλ=0.025 1 nm。减小狭缝宽度有利于提高系统的分辨率,但是随着狭缝宽度的减小,会使光强迅速减弱。因此,在不影响光强的前提下应尽可能地减小狭缝宽度,决定系统的最佳光谱带宽。过分减小狭缝宽度,光强急剧减弱且检测结果不符合光栅实际分辨率值。通过实验数据对比,在狭缝宽度为10 μm时,检测光强值最合适,检测数值也最接近光栅实际分辨率值,对应的Δλ_A如表 2所示。

图 4

Fig. 4

图 4 不同狭缝宽度检测结果对照图 Fig. 4 The test results with different widths of slits

表 2Table 2)

表 2 10 μm狭缝对应波长的ΔλA Tab. 2 The ΔλA at corresponding wavelengths with 10 μm slit width 波长/nm 365.0 404.7 435.8 546.1 577.0 579.0 ΔλA/nm 0.010 2 0.010 0 0.009 7 0.008 1 0.007 4 0.007 4

表 2 10 μm狭缝对应波长的ΔλA Tab. 2 The ΔλA at corresponding wavelengths with 10 μm slit width

假设被测光栅的参数值是:空间频率1/e=2 400 l/mm,入臂长度r_A=292.098 mm,检测波长λ=435.8 nm,出臂长度r_B=373.8 mm,狭缝宽度a=10 μm。计算狭缝宽度对光栅分辨率检测影响的光谱宽度为Δλ_A=0.009 7 nm。实际测量值为Δλ=0.017 7 nm,低压汞灯435.8 nm谱线在300 K时的多普勒增宽为δλ=0.000 38 nm,则可见光栅的实际分辨率为Δλ_r=0.007 6 nm。

因为狭缝经凹面光栅衍射后在像面上成二维光谱像,所以根据光路结构要求,为了采集到高质量的光谱像,选择面阵CCD放置于像面上采集图像。每个像素采集到的光能量用对应积累的电荷量来记录并转换成电压,经A/D转换后用数字信号输出,此时CCD能够分辨的最高空间频率等于它的空间采样频率f₀的一半,也就是光谱像在CCD的感光面上至少占两个像素。CCD的光谱分辨本领是由像素尺寸和系统的线色散率决定的。假设两个相邻像素点中心间距为p,系统的线色散率表示为 ,CCD可分辨最小波长差 ,则CCD的光谱分辨率本领为 ,由此可见CCD的光谱分辨本领与像素间距p成反比^[9]。另一方面,CCD采样信号的过程与曝光时间和增益有关,曝光时间和增益过大会导致感光面采集到的光强太强,超出像素满阱容量,像素中的电子会溢出,从而影响相邻像素点的探测采集;曝光时间和增益过小会导致感光面采集到的光强太弱,像素点积累的电荷量无法反应实际的入射光能量,所以CCD存在一个曝光时间和增益的最合适值问题。

曝光时间从8 000~2 000 ns减小,增益从32~18减小时,实验检测的像素点随曝光时间的减小而减小。同一曝光时间不同增益情况下,像素点有最佳值,当增益达到一定下限时,像素点也达到了极限数值;同一增益不同曝光时间情况下,当曝光时间达到一定下限时,像素点也有极限数值。根据实验数据,本系统曝光时间为7 000 ns,增益为23时是CCD的最佳探测模式,光强适中,像素点最合适采集到的分辨率曲线最适合数据分析。

针对上述的实验研究,利用CodeV光学设计软件,根据凹面光栅的设计要求,在宽波段模拟了罗兰圆型凹面光栅的成像系统。其光栅参数为曲率半径400.7 mm,刻线数1/e=2 400 l/mm,入射角α=-43.2°,有效口径为32 mm。凹面光栅分光光路的参数如表 3所示。

表 3Table 3)

表 3 凹面光栅分光光路参数 Tab. 3 The parameters of concave grating spectrometer 面 曲率半径/mm 间距/mm 物体 291.6 光阑 -400.7 -323 像面 400.7 0

表 3 凹面光栅分光光路参数 Tab. 3 The parameters of concave grating spectrometer

可得到仿真光路如图 5所示,入射光经光栅分光后在像面从上往下依次分布分别为579.0 nm、577.0 nm、546.1 nm、435.8nm、404.7 nm和365.0 nm的衍射光谱像,优化前生成的MTF曲线见图 6,相应波长的均方根直径RMS值如表 4所示。

图 5

Fig. 5

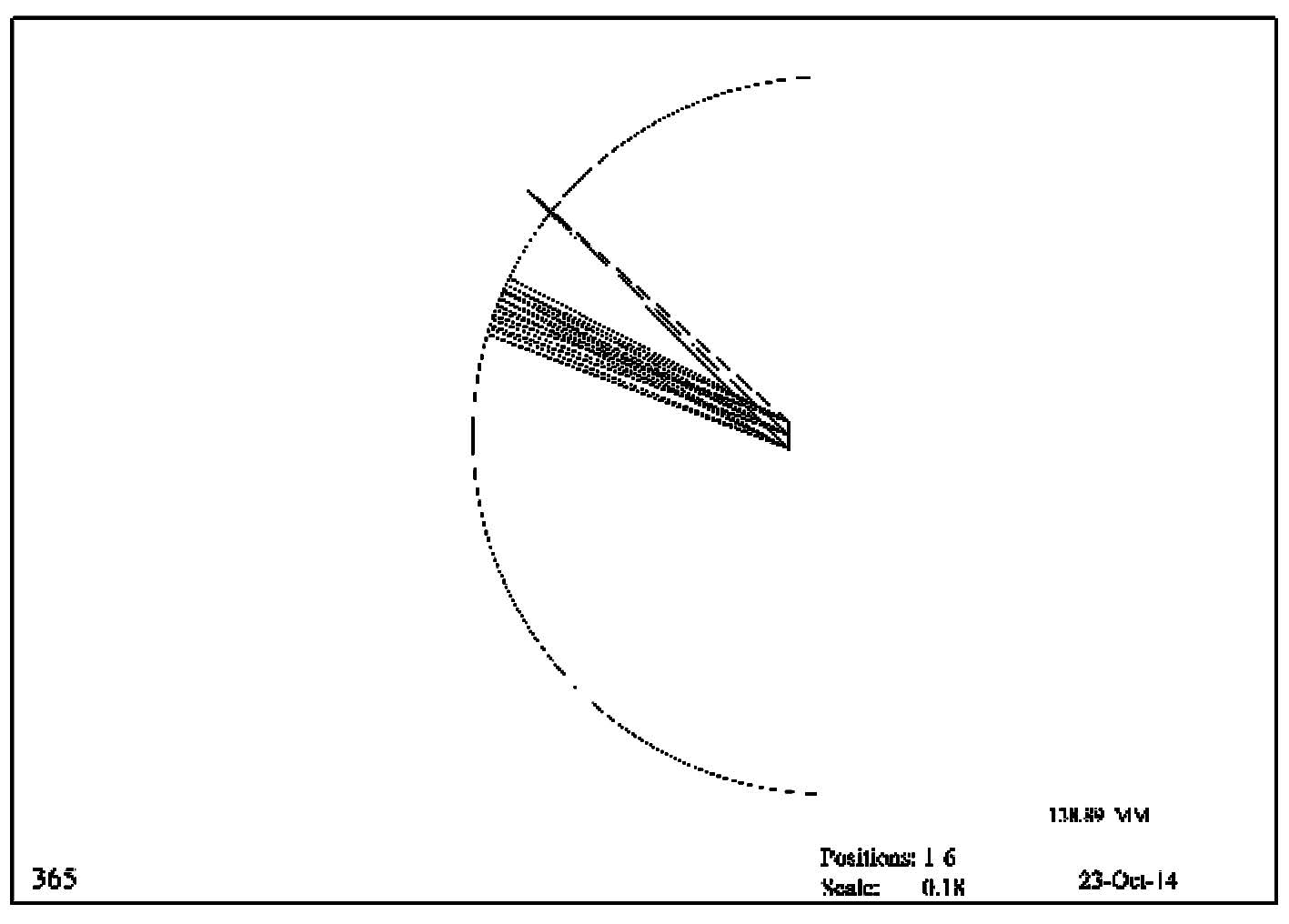图 5 优化前的凹面光栅分光示意图 Fig. 5 The spectral diagram of concave grating before optimization

图 6

Fig. 6

图 6 优化前的 MTF曲线 Fig. 6 The MTF curve before optimization

表 4Table 4)

表 4 对应波长的RMS值 Tab. 4 The RMS with corresponding wavelengths 波长/nm 365.0 404.7 435.8 546.1 577.0 579.0 RMS值/μm 14.989 14.943 14.231 11.680 10.959 10.036

表 4 对应波长的RMS值 Tab. 4 The RMS with corresponding wavelengths

RMS值是一个重要的直径参数,它是弥散斑各个点坐标与参考中心点进行坐标平方和后,除以点数量后再开方的值。该值可以典型地反映一个弥散斑的大小,以定量地反映这个系统实际的斑点大小。

由以上可以看出凹面光栅在子午面和弧矢面的成像质量与极限值均有一定的差距,具有较大像差。由其初始结构并不能得到较好的成像质量,必须对凹面光栅进行消像差优化设计,减小像差。利用CodeV软件优化,通过点列图和MTF曲线对凹面光栅的成像质量进行评估。

优化后的结果如表 5所示。

表 5Table 5)

表 5 优化后光路参数 Tab. 5 The optimized parameters of spectral optical path 面 曲率半径/mm 间距/mm 物体 292.08 光阑 -400.7 -403.25 像面 410.0 0

表 5 优化后光路参数 Tab. 5 The optimized parameters of spectral optical path

经过优化后凹面光栅的成像聚焦在像面上,如图 7所示;优化后的MTF曲线和理论极限值也较为接近,可以获得高成像质量的凹面光栅,如图 8所示;优化后相应波长的RMS值如表 6所示。

图 7

Fig. 7

图 7 优化后分光示意图 Fig. 7 The optimized spectral diagram

图 8

Fig. 8

图 8 优化后MTF曲线 Fig. 8 The optimized spectral diagram

表 6Table 6)

表 6 优化后的RMS值 Tab. 6 The optimized RMS 波长/nm 365.0 404.7 435.8 546.1 577.0 579.0 RMS值/μm 0.359 0.250 0.245 0.164 0.219 0.227

表 6 优化后的RMS值 Tab. 6 The optimized RMS

通过对比可以看出,在系统中综合考虑光源带宽、狭缝宽度及凹面光栅的像差后,检测的光栅实际分辨率贴近于光栅理论分辨率,差值在0.001 0~0.003 7 nm之间,能够真实反映光栅的实际分辨率,光栅实际分辨率和理论分辨率的差值如表 7所示。

表 7Table 7)

表 7 光栅实际分辨率和理论分辨率对比 Tab. 7 The difference between theoretical resolution and tested resolution 波长/nm d λ d l δ λ/nm Δ λ A/nm RMS值/μm 系统分辨率Δ λ/nm 光栅实际分辨率Δ λ G/nm 光栅理论分辨率Δ λ R/nm 差值/nm 365.0 1.02 ×10 -6 0.000 32 0.010 2 0.359 0 0.017 0 0.006 1 0.005 1 0.001 0 404.7 9.97 ×10 -7 0.000 36 0.010 0 0.250 0 0.017 5 0.006 9 0.005 6 0.001 3 435.8 9.71 ×10 -7 0.000 38 0.009 7 0.245 0 0.017 7 0.007 4 0.006 1 0.001 3 546.1 8.12 ×10 -7 0.000 48 0.008 1 0.164 0 0.020 0 0.011 3 0.007 6 0.003 7 577.0 7.44 ×10 -7 0.000 51 0.007 4 0.219 0 0.019 0 0.010 9 0.008 0 0.002 9 579.0 7.39 ×10 -7 0.000 51 0.007 4 0.227 0 0.018 0 0.009 9 0.008 0 0.001 9

表 7 光栅实际分辨率和理论分辨率对比 Tab. 7 The difference between theoretical resolution and tested resolution

文章首先介绍了罗兰圆型凹面光栅分辨率特性检测系统的结构及工作原理,再根据实验数据分析了光源带宽、狭缝宽度、CCD曝光时间与增益及凹面光栅的像差对分辨率检测结果造成的影响。不同光源具有不同的线性展宽,以汞灯作为标准光源,量化出扩展光源影响的理论数据。不同狭缝宽度对结果影响不同,通过实验测试数据选取最佳狭缝宽度。考虑凹面光栅的像差并进行消像差优化设计,在系统中剔除像差对光栅实际分辨率的影响,CCD调节合适的曝光时间与增益,得到凹面光栅的实际分辨率数值,这对凹面光栅的制作有着重要的参考价值。